《2022年高一數(shù)學(xué)基本算法語(yǔ)句 條件語(yǔ)句教案 新課標(biāo)》由會(huì)員分享����,可在線閱讀,更多相關(guān)《2022年高一數(shù)學(xué)基本算法語(yǔ)句 條件語(yǔ)句教案 新課標(biāo)(5頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
1���、2022年高一數(shù)學(xué)基本算法語(yǔ)句 條件語(yǔ)句教案 新課標(biāo)
教學(xué)目標(biāo):
1. 經(jīng)歷將具體問(wèn)題的流程圖轉(zhuǎn)化為偽代碼的過(guò)程�。
2. 理解用偽代碼表示的算法語(yǔ)句—條件語(yǔ)句�,進(jìn)一步體會(huì)算法的基本思想。
3. 體會(huì)算法對(duì)邏輯思維能力的鍛煉���。
二.教學(xué)過(guò)程:
昨天我們已經(jīng)在自然語(yǔ)言���、流程圖的基礎(chǔ)上學(xué)習(xí)了用于表達(dá)順序結(jié)構(gòu)的偽代碼,即輸入輸出語(yǔ)句�、賦值語(yǔ)句.那今天這節(jié)課的目標(biāo)就十分明確,是在自然語(yǔ)言、流程圖的基礎(chǔ)上學(xué)習(xí)了用于表達(dá)選擇結(jié)構(gòu)的偽代碼,即條件語(yǔ)句.
首先我們從一個(gè)熟悉的例子入手研究:
(一)目標(biāo)一: 能將具體問(wèn)題的流程圖轉(zhuǎn)化為偽代碼
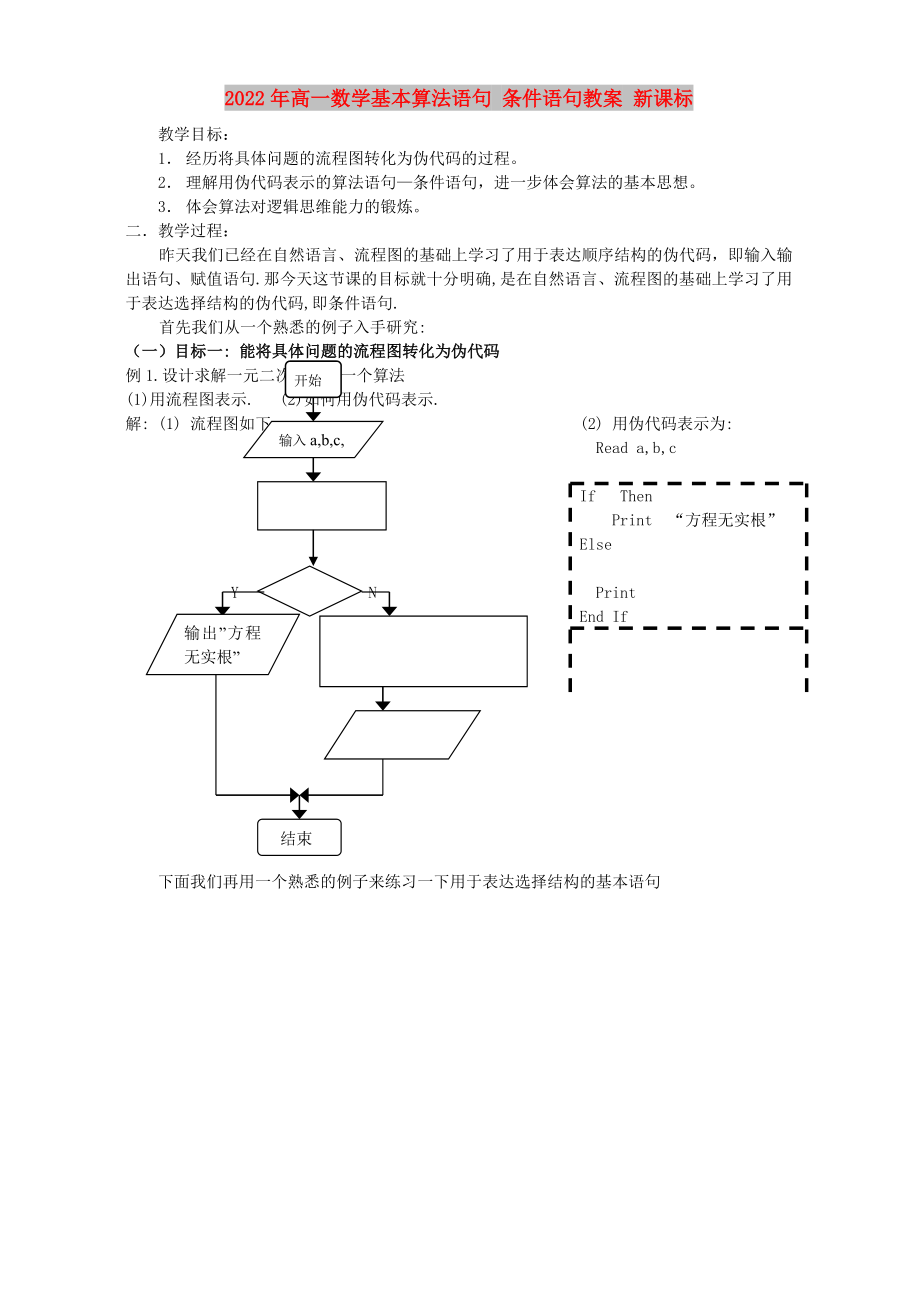
例1.設(shè)計(jì)求解一元二次方程的一個(gè)算法
(1)
2�、用流程圖表示. (2)如何用偽代碼表示.
解: (1) 流程圖如下: (2) 用偽代碼表示為:
Read a,b,c
If Then
Print “方程無(wú)實(shí)根”
3�、
Else
Y N Print
End If
輸入a,b,c,
開始
輸出”方程無(wú)實(shí)根”
4�、
結(jié)束
下面我們?cè)儆靡粋€(gè)熟悉的例子來(lái)練習(xí)一下用于表達(dá)選擇結(jié)構(gòu)的基本語(yǔ)句
輸入x
輸出y
結(jié)束
開始
例2.用偽代碼表示流程圖所描述的算法.
解: 用偽代碼表示為:
Read x
If Then
Y N
Else
End If
Print y
這兩題中的偽代碼中有十分相似的
語(yǔ)句,同學(xué)們
5、能否象第一題中用虛線框畫出來(lái).
歸納:(1)條件語(yǔ)句的一般形式: If A Then
B
Else
C
End If
(2)注意點(diǎn):①Then分支���、Else分支為了方便閱讀,一般要縮進(jìn)書寫.
②出口“ End If”表示條件語(yǔ)句結(jié)束,不能省.
(二)目標(biāo)二:能理解條件語(yǔ)句的嵌套形式
輸入x
變題:已知函數(shù),試用偽代碼寫出
計(jì)算y的
6��、一個(gè)算法.
解: (2)用偽代碼表示為: (1)流程圖為:
Read x Y Y N
If x>0 Then
Else If x=0 Then
Else
x>0
開始
x=0
輸出y
結(jié)束
End If
Print y
在上述流程圖中存在選擇結(jié)構(gòu)的嵌套形式�����,因此�,在語(yǔ)句中就存在條件語(yǔ)句的嵌套形式,
下面我們?nèi)匀辉儆靡粋€(gè)熟悉的
7���、例子來(lái)練習(xí)一下:
練習(xí)1. 用偽代碼描述流程圖所表示的算法.
解:Read a,b
If Then
Y N
Y N
Print x “是方程的根”
輸出“方程根是全體”
實(shí)數(shù)
Else If Then
Print “方程無(wú)實(shí)根”
8��、 Else
Print “方程根是全體實(shí)數(shù)”
End If
結(jié)束
輸入a,b
輸出“方程無(wú)實(shí)根”
輸出x “是
方程的根”
開始
歸納:條件語(yǔ)句的嵌套的一般形式: If Then
Else If Then
┅ ┅
Else
End If
(三)目標(biāo)三:能識(shí)別偽代碼所表示算法含義
例3.寫出下列語(yǔ)句的運(yùn)行結(jié)果:
(1) Read x
9���、 (2)Read x
If x<0 Then If Then
Print “是負(fù)數(shù)”
Else Else
End If End If
Print y P
10、rint P
若x=-4,輸出結(jié)果為 是負(fù)數(shù) 若x=6,P= 2.1
若x=9,輸出結(jié)果為 3 若x=20,P= 10.5
例4.將下列語(yǔ)句補(bǔ)充完整
(1) 判斷輸入的數(shù)是否是正數(shù), (2)求函數(shù)的函數(shù)值
若是,輸出它的平方,若不是輸出 則②為
它的相反數(shù),則①為 Read x
Read x If Then
If ① Then
11�、
Else
Else ②
End If
Print y
End If Print y
(四)目標(biāo)四:掌握算法三種表示方式的遞進(jìn)關(guān)系,并體會(huì)算法的基本思想
結(jié)束
輸出c
輸入n
開始
練習(xí)2.(應(yīng)用題1)某居民區(qū)的物
12、管部門每月按以下方法收取衛(wèi)生費(fèi):3人和3人以下的住戶,每戶收取5元;超過(guò)3人的住戶,每超出1人加收1.2元.
(1)如何設(shè)計(jì)算法,根據(jù)輸入的人數(shù)計(jì)算應(yīng)收取的費(fèi)用?
(2)根據(jù)算法畫出其流程圖. (3)根據(jù)流程圖寫出偽代碼.
解:(1)算法如下: (2)流程圖如下:
S1 輸入n
S2 若�����,則 Y N
否則
S3 輸出c
(3)用偽代碼表示為:
Read n
If Then
Else
End If
Print c
(應(yīng)用題
13、2)兒童乘火車時(shí),若身高不超過(guò)1.1米,則無(wú)需購(gòu)票;若身高超過(guò)1.1米但不超過(guò)1.4米,可購(gòu)買半票;若超過(guò)1.4米,應(yīng)買全票.
(1)如何設(shè)計(jì)購(gòu)票的算法. (2)根據(jù)算法畫出其流程圖.(3)根據(jù)流程圖寫出偽代碼.
解. (1)算法如下: (2)流程圖如下:
輸入h
開始
S1 測(cè)試兒童身高h(yuǎn)
S2 若,則免費(fèi)乘車;
否則,若,那么購(gòu)買
半票乘車;否則, 購(gòu)買全票乘車
Y
14����、 N
(3)用偽代碼表示為:
免費(fèi)乘車
Read h Y N
If Then
全票乘車
半票乘車
Print 免費(fèi)乘車
Else If Then
Print半票乘車
Else
結(jié)束
Print 全票乘車
End If
①?gòu)倪@兩個(gè)應(yīng)用題中可以看出條件語(yǔ)句對(duì)生活中一些問(wèn)題的解決是很有幫助的,這也正體現(xiàn)了生活是離不開數(shù)學(xué)的�。
②除此之外,我們還運(yùn)用了算法的三種方式來(lái)共同描述����,先用自然語(yǔ)言來(lái)描述,進(jìn)而轉(zhuǎn)化成流程圖表示��,最后再用偽代碼來(lái)表示�����。這一過(guò)程說(shuō)明這三種描述方式有內(nèi)在的遞進(jìn)關(guān)系����,這也是本章的精髓,我們要細(xì)細(xì)體會(huì)����。
(六)小結(jié):
1.會(huì)根據(jù)具體問(wèn)題寫出算法,在根據(jù)算法畫出流程圖,進(jìn)而在算法�����、流程圖基礎(chǔ)上寫出相應(yīng)的偽代碼.
2.體會(huì)這三種描述方式的遞進(jìn)關(guān)系,并體會(huì)算法的基本思想 .
3.能理解用偽代碼表示的算法語(yǔ)句.
(七)作業(yè):
 2022年高一數(shù)學(xué)基本算法語(yǔ)句 條件語(yǔ)句教案 新課標(biāo)
2022年高一數(shù)學(xué)基本算法語(yǔ)句 條件語(yǔ)句教案 新課標(biāo)