《陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 應(yīng)用舉例2典型例題素材 北師大版必修5(通用)》由會(huì)員分享����,可在線閱讀,更多相關(guān)《陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 應(yīng)用舉例2典型例題素材 北師大版必修5(通用)(4頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
1��、應(yīng)用舉例
利用正余弦定理解斜三角形�,在實(shí)際應(yīng)用中有著廣泛的應(yīng)用,如測(cè)量����、航海、幾何等方面都要用到解三角形的知識(shí)�����,例析如下:
一���、測(cè)量問題
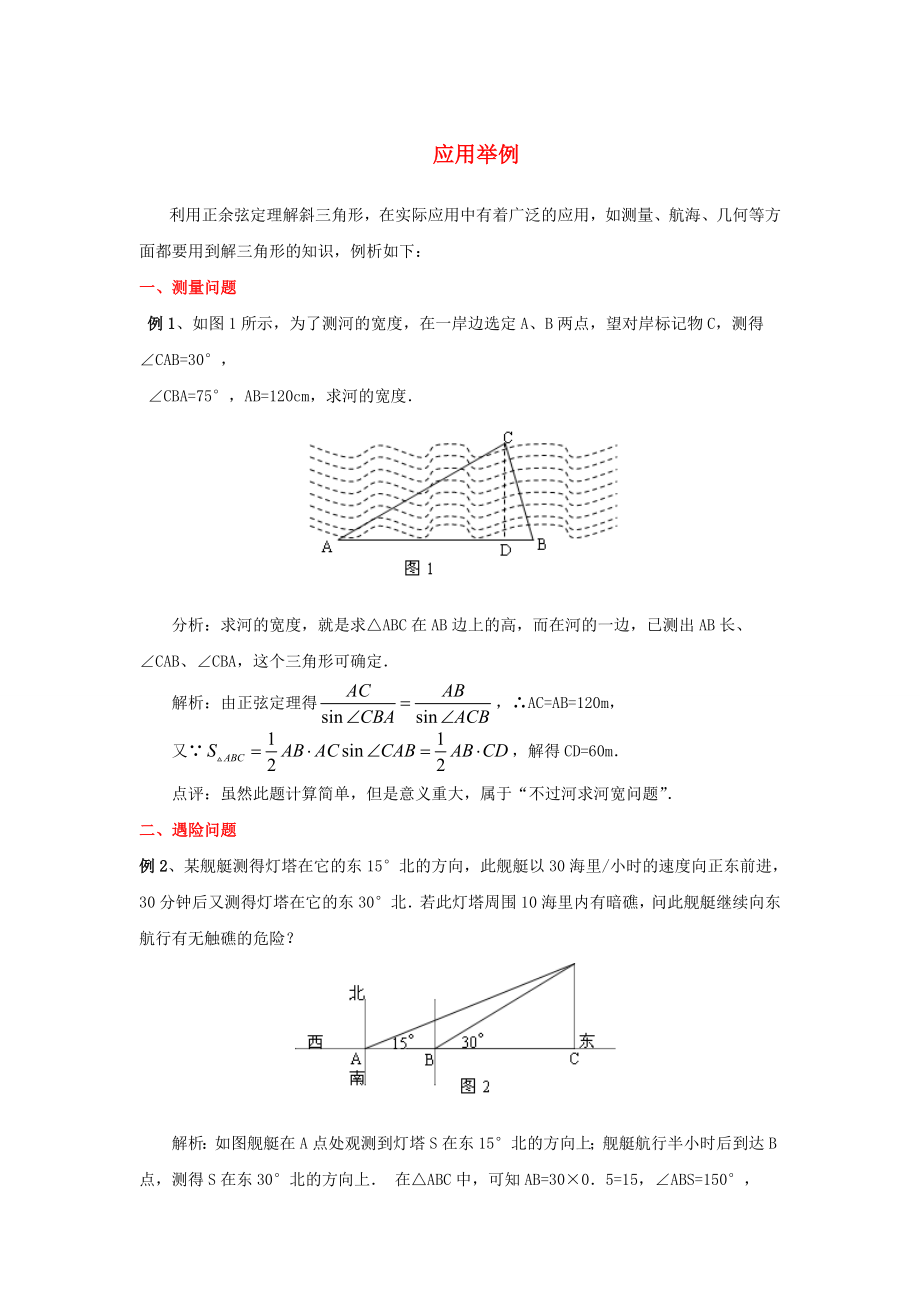
例1�、如圖1所示,為了測(cè)河的寬度�����,在一岸邊選定A����、B兩點(diǎn),望對(duì)岸標(biāo)記物C�����,測(cè)得∠CAB=30°�,
∠CBA=75°��,AB=120cm�����,求河的寬度.
分析:求河的寬度�,就是求△ABC在AB邊上的高,而在河的一邊�����,已測(cè)出AB長(zhǎng)、∠CAB����、∠CBA,這個(gè)三角形可確定.
解析:由正弦定理得�,∴AC=AB=120m,
又∵��,解得CD=60m.
點(diǎn)評(píng):雖然此題計(jì)算簡(jiǎn)單�,但是意義重大,屬于“不過河求河寬問題”.
二��、遇險(xiǎn)問題
例2�、某艦艇測(cè)得燈塔在
2、它的東15°北的方向��,此艦艇以30海里/小時(shí)的速度向正東前進(jìn)��,30分鐘后又測(cè)得燈塔在它的東30°北.若此燈塔周圍10海里內(nèi)有暗礁��,問此艦艇繼續(xù)向東航行有無觸礁的危險(xiǎn)���?
解析:如圖艦艇在A點(diǎn)處觀測(cè)到燈塔S在東15°北的方向上����;艦艇航行半小時(shí)后到達(dá)B點(diǎn),測(cè)得S在東30°北的方向上. 在△ABC中�,可知AB=30×0.5=15,∠ABS=150°�����,∠ASB=15°�����,由正弦定理得BS=AB=15����,過點(diǎn)S作SC⊥直線AB,垂足為C���,則SC=15sin30°=7.5.
這表明航線離燈塔的距離為7.5海里,而燈塔周圍10海里內(nèi)有暗礁�,故繼續(xù)航行有觸礁的危險(xiǎn).
點(diǎn)評(píng):有關(guān)斜三角形的實(shí)際問題,其解題的
3���、一般步驟是:(1)準(zhǔn)確理解題意��,分清已知與所求��,尤其要理解應(yīng)用題中的有關(guān)名詞和術(shù)語(yǔ)�����;(2)畫出示意圖����,并將已知條件在圖形中標(biāo)出;(3)分析與所研究問題有關(guān)的一個(gè)或幾個(gè)三角形�,通過合理運(yùn)用正弦定理和余弦定理求解.
三、追擊問題
例3����、如圖3,甲船在A處����,乙船在A處的南偏東45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行�����,若甲船以28n mile/h的速度航行,應(yīng)沿什么方向,用多少h能盡快追上乙船�?
解析:設(shè)用t h����,甲船能追上乙船,且在C處相遇.
在△ABC中���,AC=28t����,BC=20t�����,AB=9�����,設(shè)∠ABC=α��,∠BAC=β.
∴α=180°-
4���、45°-15°=120°.根據(jù)余弦定理,
�����,,(4t-3)(32t+9)=0�����,
解得t=�,t=(舍)∴AC=28×=21 n mile,BC=20×=15 n mile.
根據(jù)正弦定理�,得,又∵α=120°���,∴β為銳角�,β=arcsin��,又<<��,∴arcsin<���,∴甲船沿南偏東-arcsin的方向用h可以追上乙船.
點(diǎn)評(píng):航海問題常涉及到解三角形的知識(shí)�,本題中的 ∠ABC����、AB邊已知,另兩邊未知,但他們都是航行的距離��,由于兩船的航行速度已知�,所以,這兩邊均與時(shí)間t有關(guān).這樣根據(jù)余弦定理��,可列出關(guān)于t的一元二次方程����,解出t的值.
四、最值問題
例4���、某工廠生產(chǎn)主要產(chǎn)品后�,留下大量中心
5�、角為,半徑為a的扇形邊角料�����,現(xiàn)要廢物利用�,從中剪裁下巨型毛坯,要求矩形面積盡可能大����,請(qǐng)問如何裁剪?
分析:從實(shí)際出發(fā)����,盡可能使面積最大,有兩種裁剪方法.一種是使矩形的一邊落在扇形的半徑上�,另一種是使矩形的兩頂點(diǎn)分別在扇形的兩條半徑上,分別計(jì)算出這兩種情況下的最大值��,再比較結(jié)果的出最佳方案.
解:方案一��,
如圖1�,矩形有兩個(gè)頂點(diǎn)在半徑OA上,設(shè)∠AOP =����,則PM = a·sin,
∵扇形中心角為��,∴∠PQO =�����,由正弦定理��,得:=�,
即PQ =·a·sin(-)��,
∴矩形的MPQR的面積為:S=PM·PQ =·a·sin·sin(-) =·a[cos(-)-cos]≤·a·(1
6�、-) =a���,
當(dāng)=時(shí)���,cos(-) = 1,S取得最大值a.
方案二�����,如圖2�,矩形有兩個(gè)頂點(diǎn)分別在扇形的兩條半徑OA、OB上����,
設(shè)∠AOM =,∠MRA =×=�,∠MRO =,由正弦定理�����,得:=���,
即RM = 2a·sin���,
又=,∴OR = 2a·sin(-)�,∴矩形的MPQR的面積為:
S= MR·PQ = 4a·sin·sin(-) = 2a·[cos(-)-cos]
≤2a·(1-) = (2-)a.
即在此情況下,∠AOM ==時(shí)����,可求出M點(diǎn),然后作出MPQR面積為最大.
由于S-S=a-(2-)a=(-12)>0�,所以第一種方案能使裁出的矩形面積最大,即∠AOP ==�,使P取在AB弧中點(diǎn),分別向扇形的一條半徑作垂線及平行線得到矩形MPQR����,即為最大矩形.
 陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 應(yīng)用舉例2典型例題素材 北師大版必修5(通用)
陜西省吳堡縣吳堡中學(xué)高中數(shù)學(xué) 第二章 應(yīng)用舉例2典型例題素材 北師大版必修5(通用)