《人教版九年級(jí)數(shù)學(xué)下冊(cè) 第28章 銳角三角函數(shù)單元檢測(cè)試題》由會(huì)員分享�,可在線閱讀,更多相關(guān)《人教版九年級(jí)數(shù)學(xué)下冊(cè) 第28章 銳角三角函數(shù)單元檢測(cè)試題(7頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
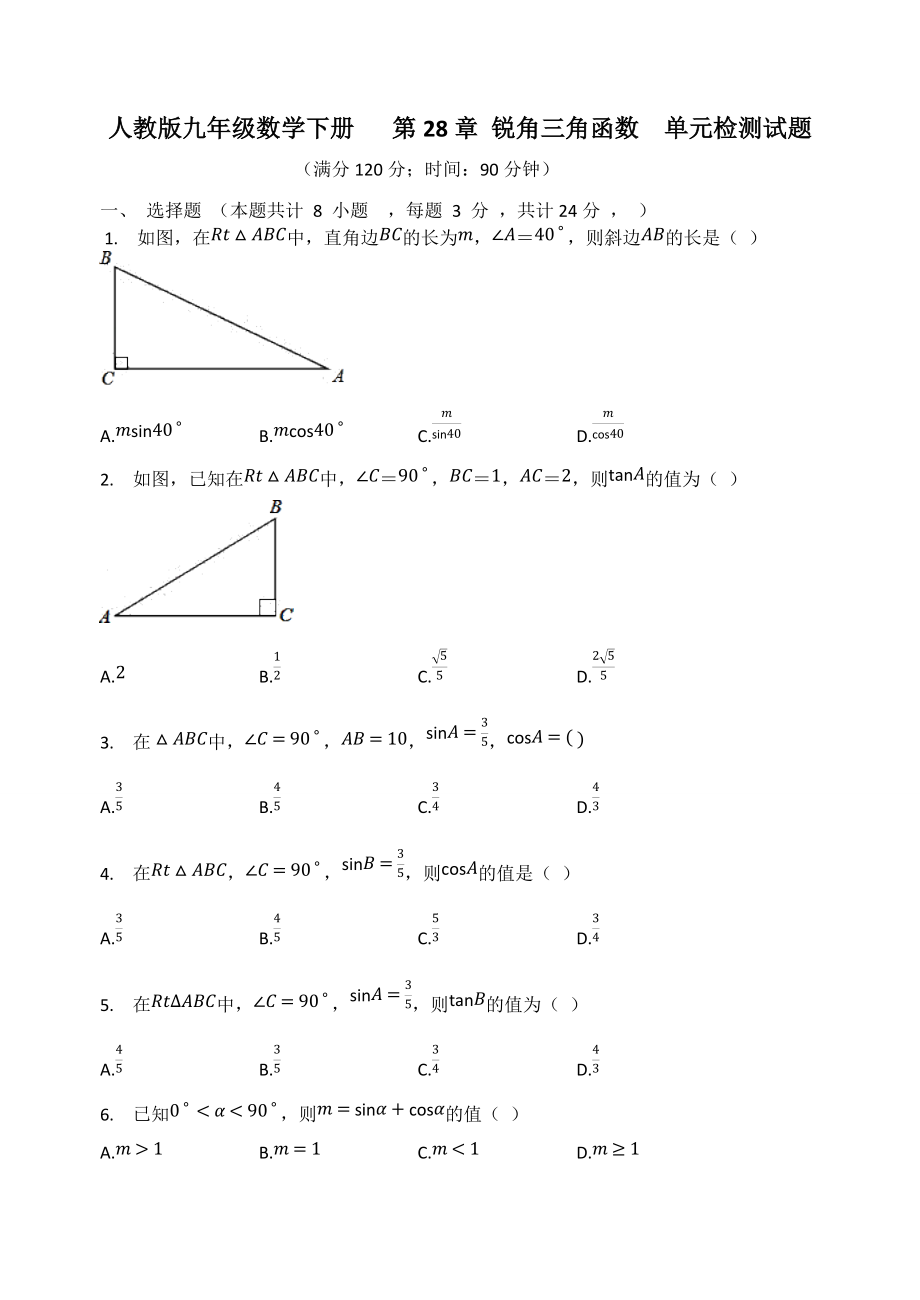
1����、人教版九年級(jí)數(shù)學(xué)下冊(cè) 第28章 銳角三角函數(shù) 單元檢測(cè)試題
(滿分120分;時(shí)間:90分鐘)
一�����、 選擇題 (本題共計(jì) 8 小題 ��,每題 3 分 ����,共計(jì)24分 , )
1. 如圖���,在Rt△ABC中�,直角邊BC的長(zhǎng)為m,∠A=40°����,則斜邊AB的長(zhǎng)是( )
A.msin40° B.mcos40° C.msin40 D.mcos40
2. 如圖,已知在Rt△ABC中�,∠C=90°,BC=1�,AC=2,則tanA的值為( )
A.2 B.12 C.55 D.255
3. 在△ABC中��,∠C=90°�����,AB=10�����,sinA=35���,cosA=( )
A.35
2、B.45 C.34 D.43
4. 在Rt△ABC����,∠C=90°�,sinB=35����,則cosA的值是( )
A.35 B.45 C.53 D.34
5. 在RtΔABC中,∠C=90°����,sinA=35,則tanB的值為( )
A.45 B.35 C.34 D.43
6. 已知0°<α<90°����,則m=sinα+cosα的值( )
A.m>1 B.m=1 C.m<1 D.m≥1
7. 如圖,甲�、乙兩艘輪船分別在P,M兩個(gè)港口?���?浚劭赑在港口M的南偏西22°方向上.某一天�,甲、乙兩艘輪船分別從P���,M兩個(gè)港口同時(shí)出發(fā)��,以相同的速度航行����,乙輪船向正南方向航行,若干小時(shí)后��,兩輪
3�、船在N處相遇,則甲輪船的航行方向是( )
A.北偏東22° B.北偏東44° C.南偏西68° D.南偏西44°
8. 如圖����,在一次“綜合實(shí)踐活動(dòng)”課上,第一小組的同學(xué)們對(duì)電桿AB的高度進(jìn)行測(cè)量���,他們?cè)诘孛嫔线x擇了三個(gè)不同的測(cè)點(diǎn)C�����,D���,E.李明同學(xué)選擇的測(cè)點(diǎn)在點(diǎn)B正南方向的C點(diǎn)處,并測(cè)得點(diǎn)A的仰角是45°�����;張磊同學(xué)選擇的測(cè)點(diǎn)在點(diǎn)B正東方向的D點(diǎn)處��,并測(cè)得點(diǎn)A的仰角是30°����;王欣同學(xué)選擇的測(cè)點(diǎn)在點(diǎn)B東南方向(即南偏東45°方向)的E點(diǎn)處,并測(cè)得點(diǎn)A的仰角是60°.測(cè)得C�����,D兩點(diǎn)之間的距離是20m���,則測(cè)點(diǎn)E和點(diǎn)B之間的距離是( )
A.10m B.5m C.1033m
4����、 D.53m
二��、 填空題 (本題共計(jì) 6 小題 �,每題 3 分 ,共計(jì)18分 ����, )
9. sin260°+cos260°?tan45°=________.
10. 如果tan(2α+10°317″)=1.7515,那么α=________.
11. 如圖,在44的正方形網(wǎng)格中����,小正方形的頂點(diǎn)稱為格點(diǎn).若△ABC的頂點(diǎn)都在格點(diǎn)上,則cos∠ABC的值是________.
12. 如圖���,網(wǎng)格中的每個(gè)小正方形的邊長(zhǎng)都是1�����,△ABC每個(gè)頂點(diǎn)都在格點(diǎn)上�����,則sinA=________.
13. 如圖��,在每個(gè)小正方形的邊長(zhǎng)為1的網(wǎng)格中�����,點(diǎn)A��,點(diǎn)B�,點(diǎn)O均落在格
5�、點(diǎn)上����,則∠AOB的正弦值為________.
14. 如圖�����,在55的正方形網(wǎng)格中����,每個(gè)小正方形的邊長(zhǎng)都是1��,△ABC的頂點(diǎn)都在這些小正方形的頂點(diǎn)上����,則cos∠BAC的值為________.
三、 解答題 (本題共計(jì) 7 小題 ��,共計(jì)78分 ����, )
15. 如圖,在修建某條地鐵時(shí)����,科技人員利用探測(cè)儀在地面A���、B兩個(gè)探測(cè)點(diǎn)探測(cè)到地下C處有金屬回聲.已知A、B兩點(diǎn)相距8米����,探測(cè)線AC,BC與地面的夾角分別是30°和45°���,試確定有金屬回聲的點(diǎn)C的深度是多少米�?
16. 如圖�����,某河堤的橫斷面是梯形ABCD���,BC?//?AD��,BE⊥AD于點(diǎn)E�����,AB=50米����,BC=3
6、0米���,∠A=60°���,∠D=30°.求AD的長(zhǎng)度.
17. 如圖,某飛艇于空中A處探測(cè)到目標(biāo)C���,此時(shí)飛行高度AC=1200米�,從飛艇上看地面控制點(diǎn)B的俯角a=30°���,求飛艇A到控制點(diǎn)B的距離AB.
18. 學(xué)校校園內(nèi)有一小山坡AB,經(jīng)測(cè)量��,坡角∠ABC=30°�����,斜坡AB長(zhǎng)為12米.為方便學(xué)生行走�,決定開挖小山坡,使斜坡BD的坡比是1:3(即為CD與BC的長(zhǎng)度之比).A�����,D兩點(diǎn)處于同一鉛垂線上,求開挖后小山坡下降的高度AD.
19. 如圖���,為了測(cè)量學(xué)校教學(xué)大樓的高度�����,小張?jiān)诰嚯x該教學(xué)大樓8米的看臺(tái)B處���,測(cè)得教學(xué)大樓樓底D的俯
7、角為37°����,測(cè)得樓頂A的仰角是60°.求該教學(xué)大樓的高度.(結(jié)果精確到0.1米,其中sin37°=0.6���,cos37°=0.8��,tan37°=0.75���,2≈1.414,3≈1.732)
20. 如圖�,已知A、B兩市相距150千米���,分別從A���、B處測(cè)得某風(fēng)景區(qū)中心C處的方位角如圖所示�����,風(fēng)景區(qū)區(qū)域是以C為圓心���,52千米為半徑的圓,tanα≈1.63����,tanβ≈1.37.有關(guān)部門要設(shè)計(jì)修建連接AB兩市的高速公路��,問(wèn)連接AB的高速公路是否穿過(guò)風(fēng)景區(qū)��,請(qǐng)說(shuō)明理由.
21. 在修建某高速公路的線路中需要經(jīng)過(guò)一座小山.如圖���,施工方計(jì)劃從小山的一側(cè)C處沿AC方向開挖隧道到小山的另一側(cè)D(A���,C,D三點(diǎn)在同一直線上)處.為了計(jì)算隧道CD的長(zhǎng)����,現(xiàn)另取一點(diǎn)B�,測(cè)得∠CAB=30°����,∠ABD=105°,AC=1km����,AB=4km.求隧道CD的長(zhǎng).
 人教版九年級(jí)數(shù)學(xué)下冊(cè) 第28章 銳角三角函數(shù)單元檢測(cè)試題
人教版九年級(jí)數(shù)學(xué)下冊(cè) 第28章 銳角三角函數(shù)單元檢測(cè)試題