2019-2020學年高中數(shù)學 第2章 平面解析幾何初步章末復習課學案 新人教B版必修2

《2019-2020學年高中數(shù)學 第2章 平面解析幾何初步章末復習課學案 新人教B版必修2》由會員分享，可在線閱讀，更多相關《2019-2020學年高中數(shù)學 第2章 平面解析幾何初步章末復習課學案 新人教B版必修2（10頁珍藏版）》請在裝配圖網(wǎng)上搜索。

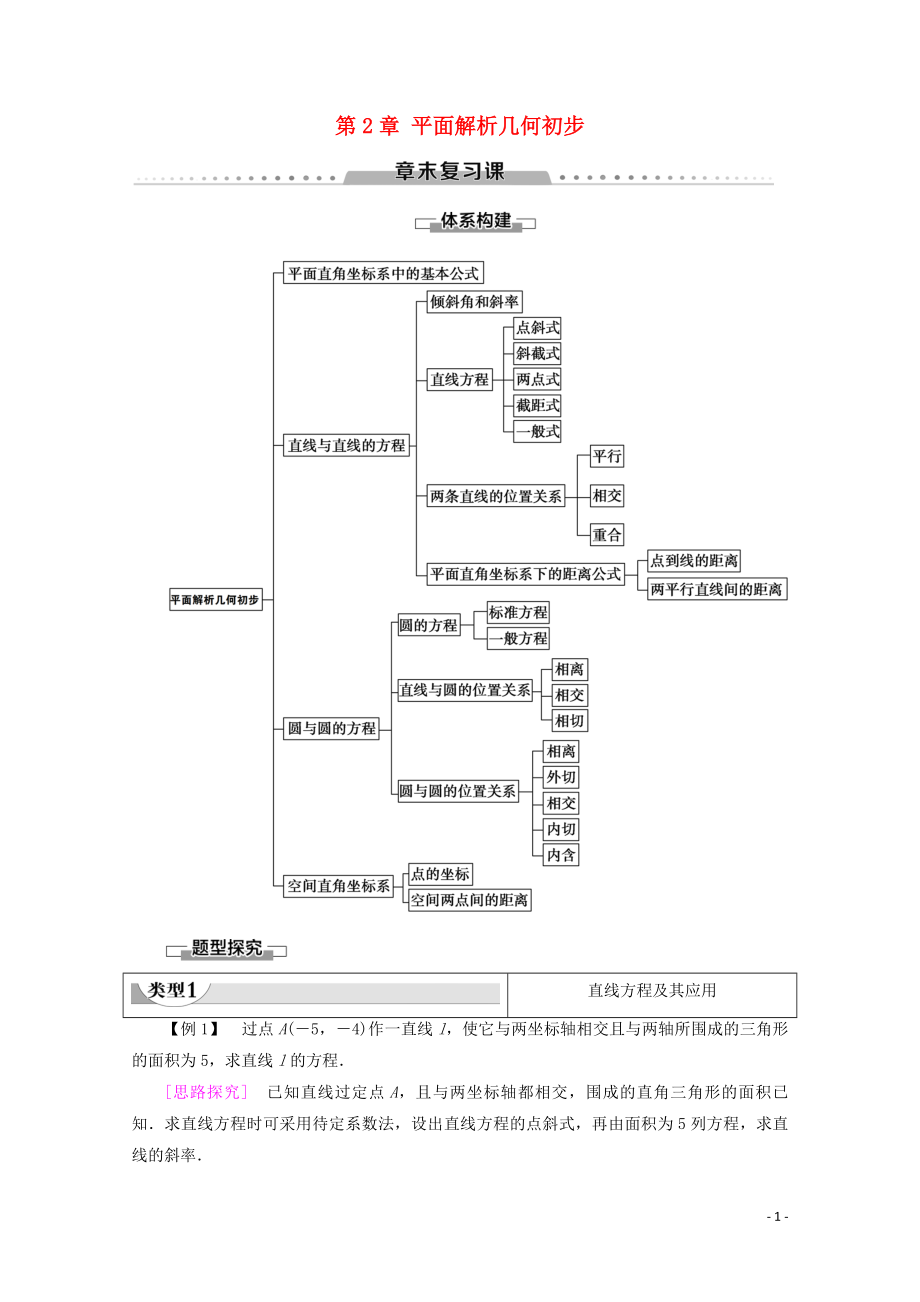
1、第2章 平面解析幾何初步 直線方程及其應用 【例1】　過點A(－5，－4)作一直線l，使它與兩坐標軸相交且與兩軸所圍成的三角形的面積為5，求直線l的方程． [思路探究]　已知直線過定點A，且與兩坐標軸都相交，圍成的直角三角形的面積已知．求直線方程時可采用待定系數(shù)法，設出直線方程的點斜式，再由面積為5列方程，求直線的斜率． [解]　由題意知，直線l的斜率存在．設直線為y＋4＝k(x＋5)，交x軸于點，交y軸于點(0，5k－4)， S＝××|5k－4|＝5， 得25k2－30k＋16＝0(無實根)，或25k2－50k＋16＝0， 解得k＝或k＝， 所以所求直線l

2、的方程為2x－5y－10＝0，或8x－5y＋20＝0. (1)求直線方程的主要方法是待定系數(shù)法，要掌握直線方程五種形式的適用條件及相互轉(zhuǎn)化，能根據(jù)條件靈活選用方程，當不能確定某種方程條件具備時要另行討論條件不滿足的情況． (2)運用直線系方程的主要作用在于能使計算簡單． 1．過點P(－1,0)，Q(0,2)分別作兩條互相平行的直線，使它們在x軸上截距之差的絕對值為1，求這兩條直線的方程． [解]　(1)當兩條直線的斜率不存在時，兩條直線的方程分別為x＝－1，x＝0，它們在x軸上截距之差的絕對值為1，滿足題意； (2)當直線的斜率存在時，設其斜率為k， 則兩條直線的方

3、程分別為y＝k(x＋1)，y＝kx＋2. 令y＝0，分別得x＝－1，x＝－. 由題意得＝1，即k＝1. 則直線的方程為y＝x＋1，y＝x＋2， 即x－y＋1＝0，x－y＋2＝0. 綜上可知，所求的直線方程為x＝－1，x＝0，或x－y＋1＝0，x－y＋2＝0. 直線的位置關系 【例2】　已知直線l1：x＋my＋6＝0，l2：(m－2)x＋3y＋2m＝0，求m的值，使得： (1)l1⊥l2；(2)l1∥l2. [思路探究]　已知兩直線的方程中都含有參數(shù)，求不同的位置關系時參數(shù)的取值，可以利用平行(或垂直)的條件列方程求解． [解]　法一：當m＝0或2時，兩直線既不平行，也不

4、垂直； 當m≠0且m≠2時，直線l1，l2的斜率分別為：－，. (1)若l1⊥l2，則－·＝－1，解得m＝. (2)若l1∥l2，則由－＝，得m＝－1或m＝3. 又當m＝3時，l1與l2重合，故m＝3舍去． 故l1∥l2時，m＝－1. 法二：(1)∵l1⊥l2，∴m－2＋3m＝0，∴m＝. (2)∵l1∥l2，∴3－m(m－2)＝0且2m≠6(m－2)， 故m＝－1. 利用直線的方程判定兩條直線的平行或垂直關系是這部分知識常涉及的題型．求解時，可以利用斜率之間的關系判定；若方程都是一般式，知道平行或垂直關系，求參數(shù)的值時也可用如下方法： 直線l1：A1x＋B1y＋C1＝

5、0， l2：A2x＋B2y＋C2＝0. (1)l1∥l2時，可令A1B2－A2B1＝0，解得參數(shù)的值后，再代入方程驗證，排除重合的情況； (2)l1⊥l2時，可利用A1A2＋B1B2＝0直接求參數(shù)的值． 2．已知點A(2,2)和直線l：3x＋4y－20＝0. (1)求過點A，且和直線l平行的直線方程； (2)求過點A，且和直線l垂直的直線方程． [解]　(1)因為所求直線與l：3x＋4y－20＝0平行， 所以設所求直線方程為3x＋4y＋m＝0. 又因為所求直線過點A(2,2)，所以3×2＋4×2＋m＝0， 所以m＝－14，所以所求直線方程為3x＋4y－14＝0.

6、 (2)因為所求直線與直線l：3x＋4y－20＝0垂直， 所以設所求直線方程為4x－3y＋n＝0. 又因為所求直線過點A(2,2)，所以4×2－3×2＋n＝0， 所以n＝－2，所以所求直線方程為4x－3y－2＝0. 距離問題 【例3】　已知兩條直線l1：ax－by＋4＝0，l2：(a－1)x＋y＋b＝0，求分別滿足下列條件的a、b的值． (1)直線l1過點(－3，－1)，并且直線l1與直線l2垂直； (2)直線l1與直線l2平行，并且坐標原點到l1、l2的距離相等． [解]　(1)∵l1⊥l2， ∴a(a－1)＋(－b)·1＝0. 即a2－a－b＝0.① 又點(－3

7、，－1)在l1上， ∴－3a＋b＋4＝0.② 由①②解得a＝2，b＝2. (2)∵l1∥l2且l2的斜率為1－a， ∴l(xiāng)1的斜率也存在，＝1－a， 即b＝. 故l1和l2的方程可分別表示為 l1：(a－1)x＋y＋＝0， l2：(a－1)x＋y＋＝0. ∵原點到l1與l2的距離相等， ∴4＝，解得a＝2或a＝. 因此或 距離公式的運用 1．距離問題包含兩點間的距離，點到直線的距離，兩平行直線間的距離． 2．牢記各類距離的公式并能直接應用，解決距離問題時，往往將代數(shù)運算與幾何圖形的直觀分析相結合． 3．已知正方形中心為點M(－1,0)，一條邊所在直線

8、的方程是x＋3y－5＝0，求其他三邊所在直線的方程． [解]　正方形中心到直線x＋3y－5＝0的距離d＝＝. 設與直線x＋3y－5＝0平行的直線方程為x＋3y＋C1＝0.由正方形的性質(zhì)，得＝， 解得C1＝－5(舍去)或C1＝7. 所以與直線x＋3y－5＝0相對的邊所在的直線方程為x＋3y＋7＝0. 設與直線x＋3y－5＝0垂直的邊所在的直線方程為 3x－y＋C2＝0.由題意，得＝， 解得C2＝9或C2＝－3. 所以另兩邊所在直線的方程為3x－y＋9＝0和3x－y－3＝0. 求圓的方程 【例4】　求圓心在直線3x＋4y－1＝0上，且經(jīng)過兩圓x2＋y2－x＋y－2＝0與x2

9、＋y2＝5的交點的圓的方程． [思路探究]　解答本題可利用過兩圓交點的圓系方程求解，也可求出兩交點坐標，再利用待定系數(shù)法求解． [解]　法一：設所求圓為x2＋y2－x＋y－2＋λ(x2＋y2－5)＝0， 化為一般式，得x2＋y2－x＋y－＝0. 故圓心坐標為， 代入直線3x＋4y－1＝0，得λ＝－. 再把λ代入所設方程，得x2＋y2＋2x－2y－11＝0， 故所求圓的方程為x2＋y2＋2x－2y－11＝0. 法二：解方程組 得兩圓的交點為A(1，－2)和B(2，－1)． 設所求圓的方程為x2＋y2＋Dx＋Ey＋F＝0. ∵A，B在圓上，且圓心在直線3x＋4y－1＝0上，

10、 ∴ 解得 ∴所求圓的方程是x2＋y2＋2x－2y－11＝0. 求圓的方程主要是聯(lián)系圓系方程、圓的標準方程和一般方程，利用待定系數(shù)法解題．一般地，當已知圓的圓心或半徑的幾何特征時，設圓的標準方程，并結合圓的幾何性質(zhì)求解；當已知圓上三個點時，設圓的一般方程；當所求圓經(jīng)過直線與圓、圓與圓的交點時，常利用圓系方程來解答． 過兩個已知圓x2＋y2＋D1x＋E1y＋F1＝0和x2＋y2＋D2x＋E2y＋F2＝0的交點的圓系方程為x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2)＝0(λ≠－1)． 4．圓心在直線5x－3y＝8上，且圓與兩坐標軸均相切，求此圓

11、的標準方程． [解]　設所求圓的標準方程為(x－x0)2＋(y－y0)2＝r2(r＞0)．因為圓與兩坐標軸均相切，故圓心坐標滿足x0－y0＝0或x0＋y0＝0. 又圓心在直線5x－3y＝8上，所以5x0－3y0＝8. 由得 由得 所以圓心坐標為(4,4)或(1，－1)，相應的半徑為r＝4或r＝1，故所求圓的標準方程為(x－4)2＋(y－4)2＝16或(x－1)2＋(y＋1)2＝1. 直線與圓、圓與圓的位置關系 【例5】　已知圓M：(x－1)2＋(y－1)2＝4，直線l過點P(2,3)且與圓M交于A，B兩點，且|AB|＝2，求直線l的方程． [思路探究]　分斜率存在與不存在兩

12、種情況： (1)???? (2)? [解]　(1)當直線l存在斜率時，設直線l的方程為y－3＝k(x－2)， 即kx－y＋3－2k＝0. 示意圖如圖，作MC⊥AB于C. 在Rt△MBC中，|BC|＝|AB|＝，|MB|＝2， 故|MC|＝＝1， 由點到直線的距離公式得＝1， 解得k＝. 故直線l的方程為3x－4y＋6＝0. (2)當直線l的斜率不存在時，其方程為x＝2， 且|AB|＝2，所以符合題意． 綜上所述，直線l的方程為3x－4y＋6＝0或x＝2. 1．直線與圓的位置關系是高考考查的重點，切線問題更是重中之重，判斷直線與圓的位置關系以幾何法為主，解題時

13、應充分利用圓的幾何性質(zhì)以簡化解題過程． 2．解決圓與圓的位置關系的關鍵是抓住它的幾何特征，利用兩圓圓心距與兩圓半徑的和、差的絕對值的大小來確定兩圓的位置關系，以及充分利用它的幾何圖形的形象直觀性來分析問題． 5．求圓O：x2＋y2＝36與圓M：x2＋y2－10y＋16＝0的公切線的方程． [解]　如圖，易知兩圓相交，公切線有兩條． 由圓M的方程易得M(0,5)，r＝3. 設兩圓的公切線與圓O相切于點B(x0，y0)， 則公切線方程為x0x＋y0y＝36. ∵點M到公切線的距離等于3， ∴＝3. ∵x＋y＝36，點M在公切線的下方， ∴－(5y0－36)＝18

14、，即y0＝.從而x0＝±＝±. 故公切線方程為x＋y－36＝0或－x＋y－36＝0， 即4x＋3y－30＝0或4x－3y＋30＝0. 軌跡問題 【例6】　如圖，圓O1與圓O2的半徑都是1，|O1O2|＝4，過動點P分別作圓O1、圓O2的切線PM，PN，(M，N分別為切點)，使得|PM|＝|PN|，試建立適當?shù)淖鴺讼?，并求動點P的軌跡方程． [思路探究]　由△PMO1與△PNO2均為直角三角形表示出切線長|PM|與|PN|，建立坐標系后，設出P點坐標即可由等式|PM|＝|PN|求出P點的軌跡方程． [解]　如圖，以O1，O2所在直線為x軸，線段|O1O2|的垂直平分線為y

15、軸，建立直角坐標系，則O1(－2,0)，O2(2,0)，設動點P的坐標為(x，y)． 在Rt△PMO1中，|PM|2＝|PO1|2－1， 在Rt△PNO2中，|PN|2＝|PO2|2－1. 又因為|PM|＝|PN|，所以|PM|2＝2|PN|2，即 |PO1|2－1＝2(|PO2|2－1)，即|PO1|2＋1＝2|PO2|2， 所以(x＋2)2＋y2＋1＝2[(x－2)2＋y2]， 整理得x2＋y2－12x＋3＝0， 即為所求點P的軌跡方程． 1．求動點的軌跡方程是解析幾何中的重要題型，解答這類問題常用的方法有：直接法、定義法、消元法、代數(shù)法等． 2．求軌跡方程的步驟

16、：(1)建系設點；(2)列出動點滿足的軌跡條件；(3)把軌跡條件坐標化；(4)化簡整理；(5)檢驗．在檢驗中要排除不符合要求的點，或者補充上漏掉的部分． 6．等腰三角形的頂點是A(4,2)，底邊一個端點是B(3,5)，求另一個端點C的軌跡方程，并說明它的軌跡是什么． [解]　設另一端點C的坐標為(x，y) . 依題意，得|AC|＝|AB|. 由兩點間距離公式， 得＝， 整理得(x－4)2＋(y－2)2＝10. 這是以點A(4,2)為圓心，以為半徑的圓，如圖所示，又因為A、B、C為三角形的三個頂點，所以A、B、C三點不共線．即點B、C不能重合且B、C不能為圓A的一直徑的兩個端點． 因為點B、C不能重合，所以點C不能為(3,5)． 又因為點B、C不能為一直徑的兩個端點，所以≠4.且≠2，即點C不能為(5，－1)． 故端點C的軌跡方程是(x－4)2＋(y－2)2＝10(除去點(3,5)和(5，－1))． 綜上，它的軌跡是以點A(4,2)為圓心，為半徑的圓，但除去(3,5)和(5，－1)兩點． - 10 -