江西省玉山縣一中2020學(xué)年高二數(shù)學(xué)上學(xué)期期中試題 文（平行班）

《江西省玉山縣一中2020學(xué)年高二數(shù)學(xué)上學(xué)期期中試題 文（平行班）》由會員分享，可在線閱讀，更多相關(guān)《江西省玉山縣一中2020學(xué)年高二數(shù)學(xué)上學(xué)期期中試題 文（平行班）（7頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

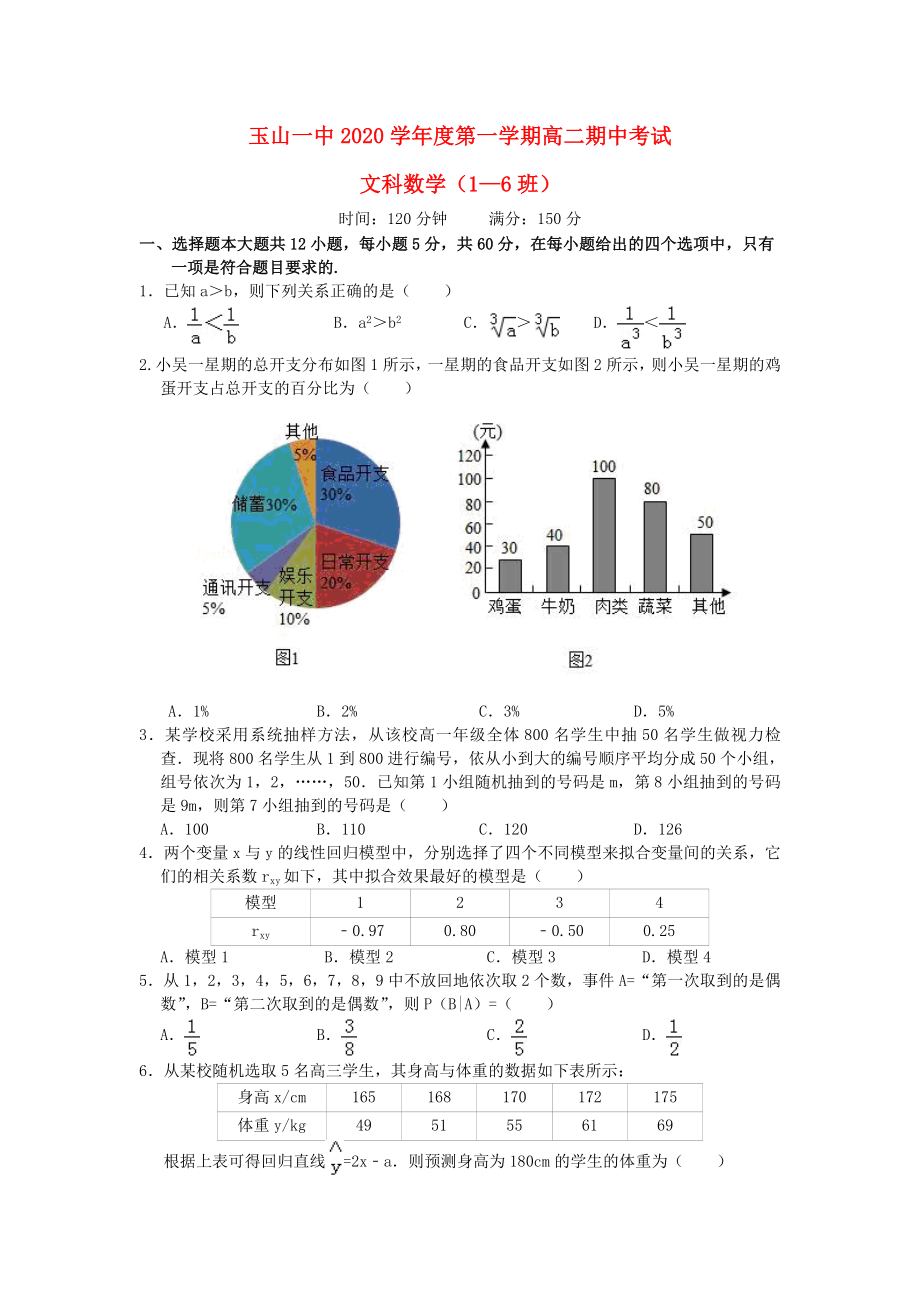
1、玉山一中2020學(xué)年度第一學(xué)期高二期中考試 文科數(shù)學(xué)（1—6班） 時間：120分鐘 滿分：150分 一、選擇題本大題共12小題，每小題5分，共60分，在每小題給出的四個選項(xiàng)中，只有一項(xiàng)是符合題目要求的. 1．已知a＞b，則下列關(guān)系正確的是（　?。? A． B．a(chǎn)2＞b2 C．＞ D．＜ 2.小吳一星期的總開支分布如圖1所示，一星期的食品開支如圖2所示，則小吳一星期的雞蛋開支占總開支的百分比為（　?。? A．1% B．2% C．3% D．5% 3．某學(xué)校采用系統(tǒng)抽樣方法，從該校高一年級全體800名學(xué)生中抽50名學(xué)生做視力檢查．現(xiàn)將800名學(xué)生從1到800進(jìn)行編號

2、，依從小到大的編號順序平均分成50個小組，組號依次為1，2，……，50．已知第1小組隨機(jī)抽到的號碼是m，第8小組抽到的號碼是9m，則第7小組抽到的號碼是（　?。? A．100 B．110 C．120 D．126 4．兩個變量x與y的線性回歸模型中，分別選擇了四個不同模型來擬合變量間的關(guān)系，它們的相關(guān)系數(shù)rxy如下，其中擬合效果最好的模型是（　?。? 模型 1 2 3 4 rxy ﹣0.97 0.80 ﹣0.50 0.25 A．模型1 B．模型2 C．模型3 D．模型4 5．從1，2，3，4，5，6，7，8，9中不放回地依次取2個數(shù)，事件A=“第一次取到的是偶數(shù)”，

3、B=“第二次取到的是偶數(shù)”，則P（B|A）=（　?。? A． B． C． D． 6．從某校隨機(jī)選取5名高三學(xué)生，其身高與體重的數(shù)據(jù)如下表所示： 身高x/cm 165 168 170 172 175 體重y/kg 49 51 55 61 69 根據(jù)上表可得回歸直線=2x﹣a．則預(yù)測身高為180cm的學(xué)生的體重為（　?。? A．73kg B．75kg C．77kg D．79kg 7．使不等式成立的x的取值范圍是（　　） A．（﹣∞，﹣1） B．（﹣1，0） C．（0，1） D．（1，+∞） 8．從一批產(chǎn)品（其中正品、次品都多于2

4、件）中任取2件,觀察正品件數(shù)和次品件數(shù)，下列事件是互斥 事件的是（ ） ①恰好有1件次品和恰好有兩件次品； ②至少有一件次品和全是次品； ③至少有1件正品和至少有1件次品； ④至少1件次品和全是正品. A.①② B. ①③ C. ③④ D. ①④ 9．設(shè)x，y滿足約束條件，向量=（x，﹣1），=（2，y﹣m），則滿足⊥的實(shí)數(shù)m的最大值（　?。? A．﹣ B．﹣ C．2 D．﹣ 10．某商場在周末推出購物滿100元贈送一次抽獎機(jī)會的活動，抽獎是這樣進(jìn)行的：一盒子內(nèi)放有大小完全相同編號為2，4，5，6，8，9的6個小球，每次從中隨機(jī)摸出

5、3個小球．若這3個小球的編號可以構(gòu)成等比數(shù)列，則獲得一等獎：若這3個小球的編號可以構(gòu)成等差數(shù)列，則獲得二等獎．在此次抽獎活動中，獲得一等獎與二等獎的概率分別為（　　） A．， B．， C．， D．， 11.觀察下列各式：31=3，32=9，33=27，34=81，…，則32020的末位數(shù)字為（　?。? A．1 B．3 C．7 D．9 12．若不等式x2﹣2ax+a＞0對一切實(shí)數(shù)x∈R恒成立，則關(guān)于t的不等式loga（t2+2t﹣2）＞0的解集為（　?。? A．（﹣3，1） B． C．

6、 D． 二、填空題（本大題共4小題，每小題5分，共20分，把答案填在答題卡對應(yīng)的橫線上）. 13．在半徑為2的圓O內(nèi)任取一點(diǎn)P，則點(diǎn)P到圓心O的距離大于1的概率為　 ?。? 14．執(zhí)行如圖程序框圖，則輸出的n等于　 ?。? 15．已知a＞0，b＞0，且+=1，則3a+2b+的最小值等于　 ?。? 16．用火柴棒擺“金魚”，如圖所示： 按照上面的規(guī)律，第336個“金魚”圖需要火柴棒的根數(shù)為　 　． 三、解答題（本大題共6小題，共70分） 17．已知函數(shù)f（x）=x2﹣2x+2． （1）求不等式f（x）＞10的解集； （2）若不等式f（x）＞2x2+a

7、x+b的解集是（﹣2，3），求實(shí)數(shù)a，b的值． 18．某城市100戶居民的月平均用電量（單位：度）以[160，180）、[180，200）、[200，220）、 [220，240）、[240，260）、[260，280）、[280，300）分組的頻率分布直方圖如圖所示： （1）求直方圖中x的值； （2）用分層抽樣的方法從[260，280）和[280，300）這兩組用戶中確定6人做隨訪，再從這6人中隨 機(jī)抽取2人做問卷調(diào)查，則這2人來自不同組的概率是多少？ （3）求月平均用電量的眾數(shù)和中位數(shù)． 19.已知x，y滿足約束條件 （1）求的取值范圍．

8、（2）若目標(biāo)函數(shù)z=ax+y取得最大值的最優(yōu)解有無窮多個，求a的值． 　 20．某學(xué)生對其親屬30人的飲食習(xí)慣進(jìn)行一次調(diào)查，并用如圖所示的莖葉圖表示30人的飲食指數(shù) （說明：圖中飲食指數(shù)低于70的人，飲食以蔬菜為主；飲食指數(shù)高于70的人，飲食以肉類為主） （1）根據(jù)以上數(shù)據(jù)完成下列2×2列聯(lián)表． 主食蔬菜 主食肉食 總計(jì) 50歲以下 50歲以上 總計(jì) （2）能否有99%的把握認(rèn)為其親屬的飲食習(xí)慣與年齡有關(guān)？并寫出簡要分析． 21．設(shè)函數(shù)． （1）若對于一切實(shí)數(shù)，恒成立，求的取值范圍； （2）對于恒成立，

9、求的取值范圍 22．已知函數(shù). ①分別求； ②由①中計(jì)算的結(jié)果歸納猜想一般性結(jié)論， ③證明②中的一般性結(jié)論． 高二文科數(shù)學(xué)1-6班參考答案 一、選擇題 1-5 CCBAB 6-12 CCDCD DB 二、填空題 13-16 3 11 2020 三、解答題 17. 【解答】解：（1）∵函數(shù)f（x）=x2﹣2x+2，不等式f（x）＞10， ∴x2﹣2x+2＞10，∴x2﹣2x﹣8＞0， 解得x＜﹣2或x＞4， ∴不等式f（x）＞10的解集為（﹣∞，﹣2）∪（4，+∞）． （2）∵不等式

10、f（x）＞2x2+ax+b的解集是（﹣2，3）， ∴x2+（a+2）x+b+2＜0的解集是（﹣2，3）， ∴﹣2和3是方程x2+（a+2）x+b+2=0的兩個實(shí)數(shù)根， ∴， 解得a=﹣3，b=﹣4． 18. 解：（1）根據(jù)頻率和為1，得 （0.002+0.0095+0.010+0.0125+x+0.005+0.0025）×20=1，解得x=0.0075； （2）根據(jù)[260，280）和[280，300）這兩組用戶的頻率比為2：1， 從中抽取6人，[260，280]中抽取4人，記為a、b、c、d， [280，300]中抽取2人，記為E、F， 再從這6人中隨機(jī)抽取2人，基本事件

11、為： ab、ac、ad、aE、aF、bc、bd、bE、bF、cd、cE、cF、dE、dF、EF共15種； 這2人來自不同組的基本事件為： aE、aF、bE、bF、cE、cF、dE、dF共8種； 故所求的概率為P=； （3）根據(jù)頻率分布直方圖知，眾數(shù)為×（220+240）=230； 由（0.002+0.0095+0.011）×20=0.45＜0.5， ∴中位數(shù)應(yīng)在[220，240]內(nèi)，可設(shè)為x，則 0.45+（x﹣220）×0.0125=0.5， 解得x=224， ∴中位數(shù)為224． 19.解：（1）z==，可看作區(qū)域內(nèi)的點(diǎn)（x，y）與點(diǎn)D（﹣5，﹣5）連線的斜率， 由圖

12、可知，kBD≤z≤kCD．即 （2）一般情況下，當(dāng)z取得最大值時，直線所經(jīng)過的點(diǎn)都是唯一的，但若直線平行于邊界直線，即直線z=ax+y平行于直線3x+5y=30時，線段BC上的任意一點(diǎn)均使z取得最大值，此時滿足條件的點(diǎn)即最優(yōu)解有無數(shù)個．又kBC=﹣，∴﹣a=﹣，∴a=． 20. 解：（1）由莖葉圖中數(shù)據(jù)，填寫列聯(lián)表如下； 主食蔬菜 主食肉食 總計(jì) 50歲以下 4 8 12 50歲以上 16 2 18 總計(jì) 20 10 30 （2）由表中數(shù)據(jù)，計(jì)算K2==10＞6.635， 所以有99%的把握認(rèn)為親屬的飲食習(xí)慣與年齡有關(guān)． 21. 解：（1）若m=

13、0，f（x）=﹣＜0顯然成立； 若m≠0，則，解得﹣6＜m＜0，綜上，m的取值范圍是（﹣6，0]； （2）要使在x∈[1，3]恒成立， 只需滿足m（x2﹣x+1）＜4在x∈[1，3]恒成立；因?yàn)椋? 所以對于x∈[1，3]恒成立；設(shè)， 則m＜g（x）min；因?yàn)椋裕? 所以m的取值范圍是（﹣∞，）． 22. 解：①函數(shù)f（x）=，∴f（0）+f（1）===， f（﹣1）+f（2）=+=+=， f（﹣2）+f（3）=+=+=．..................（6分）． ②由①猜想：．...............................................................8分 證明：②設(shè)x1+x2=1，則f（x1）+f（x2）===．...（12分）．