《人教版八下數(shù)學(xué) 期末重點(diǎn)強(qiáng)化3 四邊形計(jì)算(一)求長度的常用方法》由會(huì)員分享,可在線閱讀��,更多相關(guān)《人教版八下數(shù)學(xué) 期末重點(diǎn)強(qiáng)化3 四邊形計(jì)算(一)求長度的常用方法(3頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1�����、
人教版八下數(shù)學(xué) 期末重點(diǎn)強(qiáng)化3 四邊形計(jì)算(一)求長度的常用方法
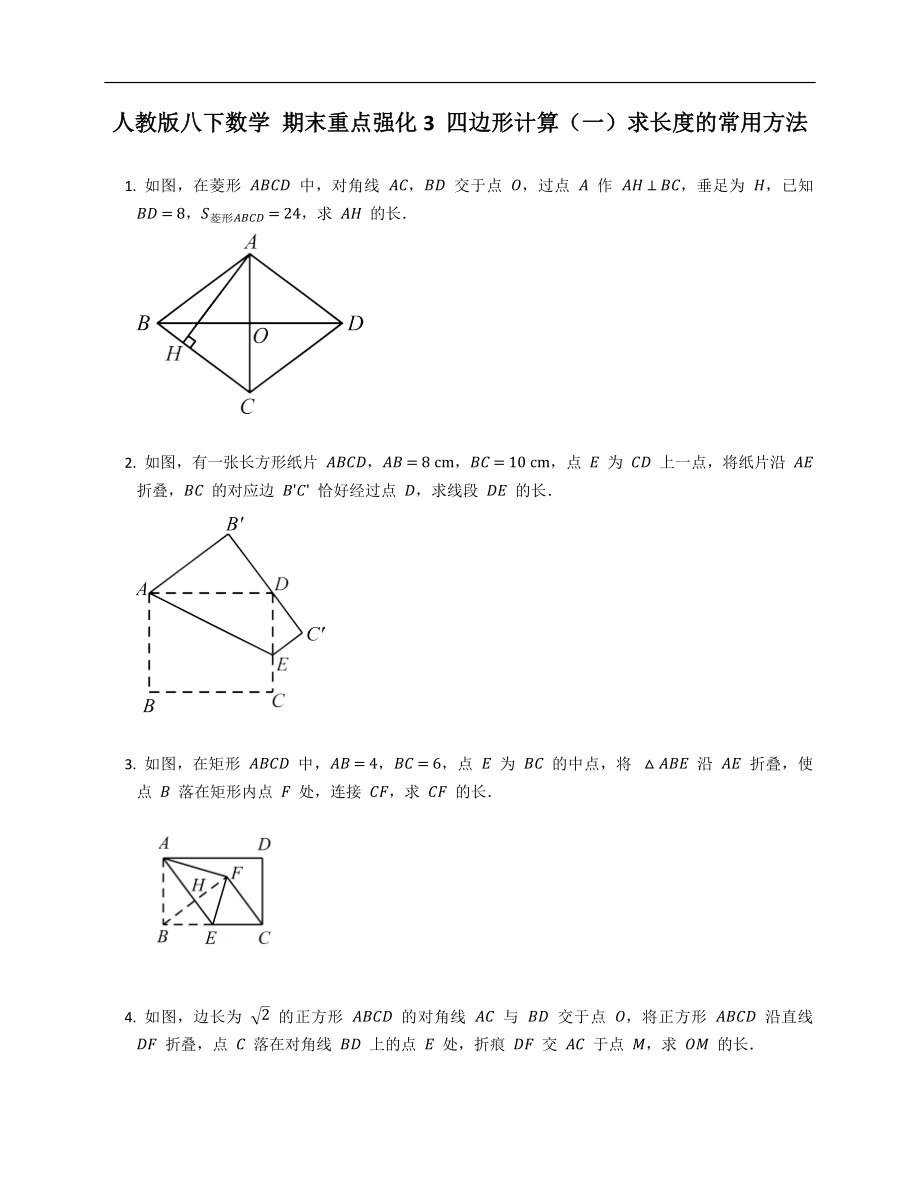
1. 如圖��,在菱形 ABCD 中����,對(duì)角線 AC�,BD 交于點(diǎn) O����,過點(diǎn) A 作 AH⊥BC,垂足為 H�,已知 BD=8����,S菱形ABCD=24����,求 AH 的長.
2. 如圖����,有一張長方形紙片 ABCD��,AB=8?cm,BC=10?cm��,點(diǎn) E 為 CD 上一點(diǎn)����,將紙片沿 AE 折疊�����,BC 的對(duì)應(yīng)邊 B?C? 恰好經(jīng)過點(diǎn) D,求線段 DE 的長.
3. 如圖�,在矩形 ABCD 中���,AB=4����,BC=6�����,點(diǎn) E 為 BC 的中點(diǎn)���,將 △ABE 沿 AE 折疊����,使點(diǎn) B 落在矩形內(nèi)點(diǎn) F 處���,連接 CF���,
2���、求 CF 的長.
4. 如圖,邊長為 2 的正方形 ABCD 的對(duì)角線 AC 與 BD 交于點(diǎn) O�����,將正方形 ABCD 沿直線 DF 折疊,點(diǎn) C 落在對(duì)角線 BD 上的點(diǎn) E 處���,折痕 DF 交 AC 于點(diǎn) M,求 OM 的長.
答案
1. 【答案】 S菱形ABCD=12BD?AC=24,BD=8����,
∴AC=6.
∵ 四邊形 ABCD 是菱形����,
∴AO=OC=3�,BO=OD=4����,AC⊥BD����,
∴BC=OB2+OC2=5,
∴S菱形ABCD=BC?AH=24��,AH=4.8.
2. 【答案】 ∵ 長方形紙片 ABCD�����,AB=8,BC=10�,
∴
3��、AB?=8�,AD=10�����,B?C?=10.
在 Rt△ADB? 中,由勾股定理�����,得 DB?=6.
∴DC?=4.
設(shè) DE=x���,則 CE=C?E=8-x.
在 Rt△C?DE 中��,由勾股定理,得 DE2=EC?2+DC?2,
即 x2=8-x2+42�,
∴x=5��,即線段 DE 的長為 5?cm.
3. 【答案】連接 BF,
∵BC=6��,點(diǎn) E 為 BC 的中點(diǎn),
∴BE=3���,
又 ∵AB=4���,
∴AE=AB2+BE2=5,由面積法可得 BH=125�,則 BF=245��,
∵FE=BE=EC,
∴∠BFC=90°���,
∴CF=62-2452=185.
4. 【答案】 ∵ 四邊形 ABCD 是正方形����,
∴AB=AD=BC=CD=2�,∠DCB=∠COD=∠BOC=90°��,OD=OC�����,
∴BD=2AB=2��,
∴OD=BO=OC=1
∵ 將正方形 ABCD 沿直線 DF 折疊,點(diǎn) C 落在對(duì)角線 BD 上的點(diǎn) E 處�����,
∴DE=DC=2���,DF⊥CE�����,
∴OE=2-1����,∠EDF+∠FED=∠ECO+∠OEC=90°,
∴∠ODM=∠ECO����,
∴△OEC≌△OMDASA����,
∴OM=OE=2-1.
 人教版八下數(shù)學(xué) 期末重點(diǎn)強(qiáng)化3 四邊形計(jì)算(一)求長度的常用方法
人教版八下數(shù)學(xué) 期末重點(diǎn)強(qiáng)化3 四邊形計(jì)算(一)求長度的常用方法