2018年高中數(shù)學 第三章 變化率與導數(shù) 3.2.2 導數(shù)的幾何意義課件7 北師大版選修1 -1.ppt

《2018年高中數(shù)學 第三章 變化率與導數(shù) 3.2.2 導數(shù)的幾何意義課件7 北師大版選修1 -1.ppt》由會員分享，可在線閱讀，更多相關《2018年高中數(shù)學 第三章 變化率與導數(shù) 3.2.2 導數(shù)的幾何意義課件7 北師大版選修1 -1.ppt（20頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、導數(shù)的幾何意義,復習：,1、函數(shù)的平均變化率,2、函數(shù)在某一點處的導數(shù)的定義 （導數(shù)的實質）,3、函數(shù)的導數(shù)、瞬時變化率、 平均變化率的關系,如圖：PQ叫做曲線的割線 那么，它們的 橫坐標相差（ ） 縱坐標相差（ ）,導數(shù)的幾何意義:,斜率,當Q點沿曲線靠近P時，割線PQ怎么變化？x呢？ y呢？,,,,,,P,Q,,,,,,,,切線,T,導數(shù)的幾何意義:,我們發(fā)現(xiàn),當點Q沿著曲線無限接近點P即x0時,割線PQ如果有一個極限位置PT.則我們把直線PT稱為曲線在點P處的切線.,設切線的傾斜角為,那么當x0時,割線PQ的斜率,稱為曲線在點P處的切線的斜率.,即:,這個概念: 提供了求曲線上某

2、點切線的斜率的一種方法; 切線斜率的本質函數(shù)在x=x0處的導數(shù).,,【例1】 求曲線y=x2在點P(1,1)處的切線的方程。,,k=,,,解： y=f(1+ x)-f(1),= (1+ x)2 -1,=2 x+（ x）2,曲線在點P(1,1)處的切線的斜率為,因此，切線方程為 y-1=2(x-1),即： y=2x-1,（4）根據(jù)點斜式寫出切線方程,求 斜 率,【總結】求曲線y=f(x)在點P(x0,f(x0))處的切線的方法：,(1)求y=f(x0+ x)-f(x0),,k=,,練習:如圖已知曲線 ,求: (1)點P處的切線的斜率; (2)點P處的切線方程.,即點P處

3、的切線的斜率等于4.,(2)在點P處的切線方程是y-8/3=4(x-2),即12x-3y-16=0.,在不致發(fā)生混淆時，導函數(shù)也簡稱導數(shù),函數(shù)導函數(shù),由函數(shù)f(x)在x=x0處求導數(shù)的過程可以看到,當時,f(x0) 是一個確定的數(shù).那么,當x變化時,便是x的一個函數(shù),我們叫它為f(x)的導函數(shù).即:,,,【例2】,,k=,(5)根據(jù)點斜式寫出切線方程,【總結】求過曲線y=f(x)外點P(x1,y1)的切線的步驟：,,k=,(1) 設切點(x0，f (x0)),(3) 用(x0，f (x0))， P(x1,y1)表示斜率,(4) 根據(jù)斜率相等求得x0，然后求得斜率k,（3）函數(shù)f(x)在點x0處

4、的導數(shù) 就是導函數(shù) 在x=x0處的函數(shù)值，即 。這也是 求函數(shù)在點x0處的導數(shù)的方法之一。,（2）函數(shù)的導數(shù)，是指某一區(qū)間內(nèi)任意點x而言的, 就是函數(shù)f(x)的導函數(shù) 。,（1）函數(shù)在一點處的導數(shù)，就是在該點的函數(shù)的改 變量與自變量的改變量之比的極限，它是一個 常數(shù)，不是變數(shù)。,1.弄清“函數(shù)f(x)在點x0處的導數(shù)”、“導函數(shù)”、“導數(shù)” 之間的區(qū)別與聯(lián)系。,小結,隨堂檢測： 1.已知曲線y=2x2上一點A(1,2)，求 （1）點A處的切線的斜率； （2）點A處的切線方程。 2.求曲線y=x2+1在點P(-2,5)處的切 線的方程。,3、求

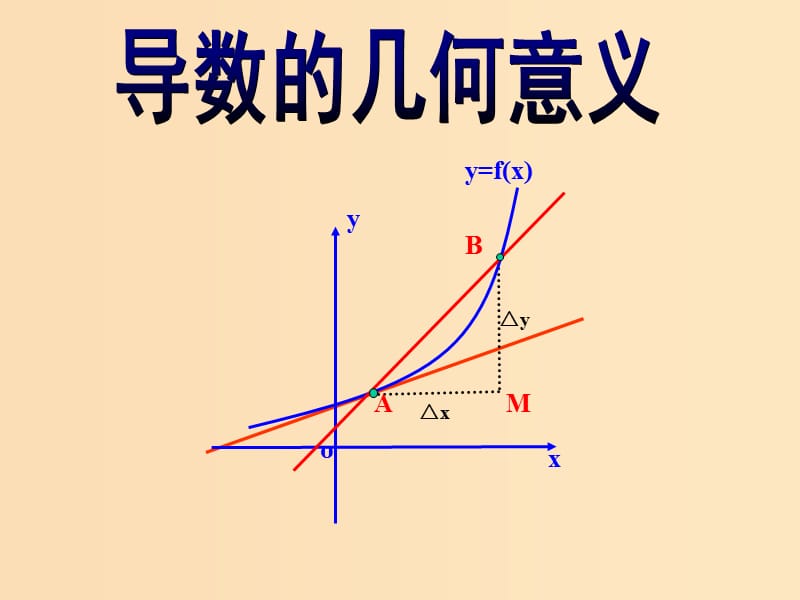
5、曲線y=x-1過點(2,0)的切線方程,,3、求曲線y=x-1過點(2,0)的切線方程,4、曲線 在點M處的切 線的斜率為2，求點M的坐標。,5、在曲線 上求一點，使過該點的切線與直線 平行。,思考與探究,曲線在某一點處的切線只能與曲線有唯一公共點嗎？下圖中，直線是否是曲線在點P處的切線？,,,謝謝大家,謝謝大家,,設曲線C是函數(shù)y=f(x)的圖象，,在曲線C上取一點A(x0,y0),及鄰近一,,點B(x0+x,y0+y),,過A、B兩點作割,線，,當點B沿著曲線無限接近于點A,點A處的切線。,即x0時, 如果割線AB有一個極,限位置AD, 那么直線AD叫做曲線在,曲線在某一點處的切線的定義,,,,,,,,D,,,設割線AB的傾斜角為， 切線AD的傾斜角為,當x0時，割線AB的 斜率的極限，就是曲線在點P 處的切線的斜率，即,tan =,,,D,,x,y,曲線在某一點處的切線的斜率公式,,,x,o,y,,y=f(x),,B,,tan=,