《（普通班）高三數(shù)學(xué)一輪復(fù)習(xí) 第十四篇 不等式選講 第2節(jié) 證明不等式的基本方法基礎(chǔ)對(duì)點(diǎn)練 理-人教版高三全冊(cè)數(shù)學(xué)試題》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《（普通班）高三數(shù)學(xué)一輪復(fù)習(xí) 第十四篇 不等式選講 第2節(jié) 證明不等式的基本方法基礎(chǔ)對(duì)點(diǎn)練 理-人教版高三全冊(cè)數(shù)學(xué)試題（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、第2節(jié) 證明不等式的基本方法
【選題明細(xì)表】
知識(shí)點(diǎn)、方法
題號(hào)
比較法證明不等式
1
綜合法證明不等式
3
分析法證明不等式
2
分析綜合法證明不等式
4
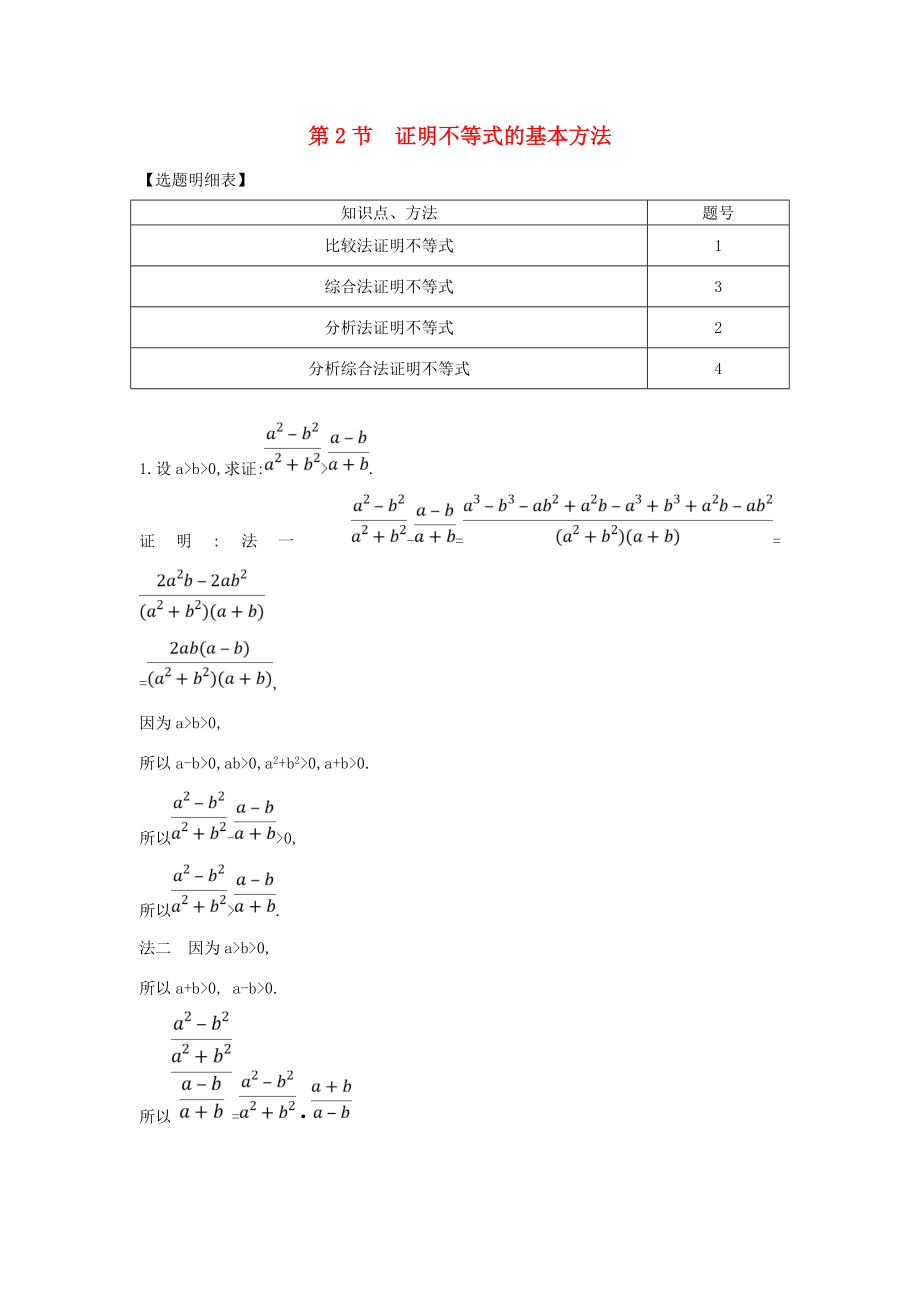
1.設(shè)a>b>0,求證:>.
證明:法一 -==
=,
因?yàn)閍>b>0,
所以a-b>0,ab>0,a2+b2>0,a+b>0.
所以->0,
所以>.
法二 因?yàn)閍>b>0,
所以a+b>0, a-b>0.
所以=·
=
=
=1+>1.
所以>.
2.設(shè)x≥1,y≥1,求證x+y+≤++xy.
證明:由于x≥1,y≥1,
要證x+y+≤++xy,
只需證xy(x+y)+1≤
2、y+x+(xy)2.
因?yàn)閇y+x+(xy)2]-[xy(x+y)+1]
=[(xy)2-1]-[xy(x+y)-(x+y)]
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1),
由條件x≥1,y≥1,
所以(xy-1)(x-1)(y-1)≥0,
從而所要證明的不等式成立.
3.(2015高考湖南卷)設(shè)a>0,b>0,且a+b=+.證明:
(1)a+b≥2;
(2)a2+a<2與b2+b<2不可能同時(shí)成立.
證明:由a+b=+=,a>0,b>0,
得ab=1.
(1)由基本不等式及ab=1,
有a+b≥2=2,
即a+b≥2.
(2)假設(shè)a2+a<2與b2+b<2同時(shí)成立,
則由a2+a<2及a>0得00,b>0,c>0,求證:++≥.
證明:要證++≥,
只需證+1++1++1≥,
只需證++≥,
只需證(a+b+c) (++)≥.
因?yàn)?a+b+c) (++)
=[ (b+c)+(a+c)+(a+b)]·(++)≥×3×3×=,當(dāng)且僅當(dāng)a=b=c時(shí)“=”成立,
故原不等式成立.
（普通班）高三數(shù)學(xué)一輪復(fù)習(xí) 第十四篇 不等式選講 第2節(jié) 證明不等式的基本方法基礎(chǔ)對(duì)點(diǎn)練 理-人教版高三全冊(cè)數(shù)學(xué)試題
