《河北省二十冶綜合學(xué)校高考數(shù)學(xué)總復(fù)習(xí) 正態(tài)分布教案》由會(huì)員分享，可在線閱讀，更多相關(guān)《河北省二十冶綜合學(xué)校高考數(shù)學(xué)總復(fù)習(xí) 正態(tài)分布教案（3頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、
河北省二十冶綜合學(xué)校高中分校高考數(shù)學(xué)總復(fù)習(xí) 正態(tài)分布教案
教學(xué)目標(biāo)：掌握正態(tài)分布在實(shí)際生活中的意義和作用 ，結(jié)合正態(tài)曲線，加深對(duì)正態(tài)密度函數(shù)的理理，通過正態(tài)分布的圖形特征，歸納正態(tài)曲線的性質(zhì)
教學(xué)重點(diǎn)：正態(tài)分布曲線的性質(zhì)。
教學(xué)難點(diǎn)：通過正態(tài)分布的圖形特征，歸納正態(tài)曲線的性質(zhì)。
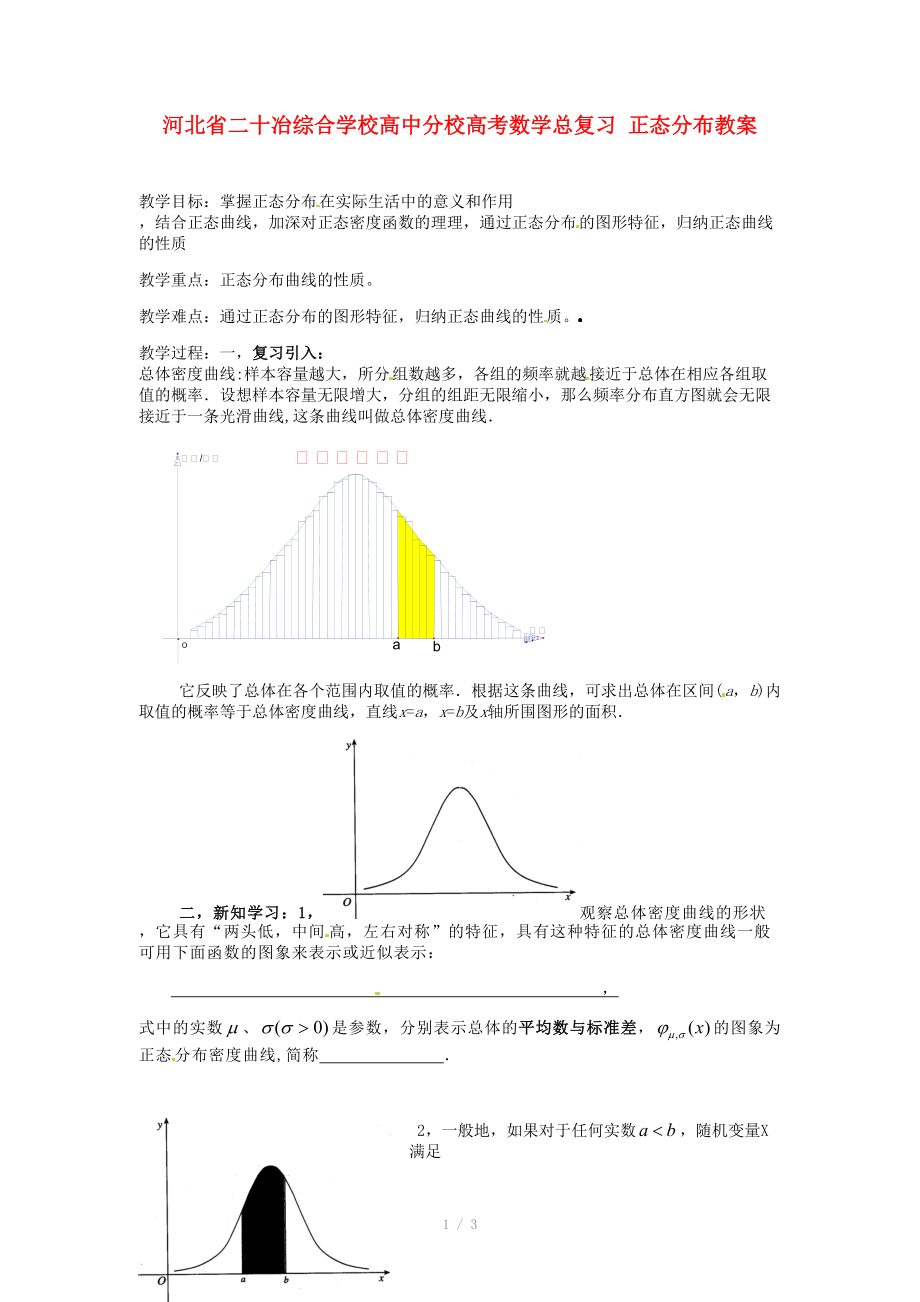
教學(xué)過程：一，復(fù)習(xí)引入： 總體密度曲線:樣本容量越大，所分組數(shù)越多，各組的頻率就越接近于總體在相應(yīng)各組取值的概率．設(shè)想樣本容量無限增大，分組的組距無限縮小，那么頻率分布直方圖就會(huì)無限接近于一條光滑曲線,這條曲線叫做總體密度曲線．
它反映了總體在各個(gè)范圍內(nèi)取值的概率．根據(jù)這條曲線，可求出總體在區(qū)間
2、(a，b)內(nèi)取值的概率等于總體密度曲線，直線x=a，x=b及x軸所圍圖形的面積．
二，新知學(xué)習(xí)：1，觀察總體密度曲線的形狀，它具有“兩頭低，中間高，左右對(duì)稱”的特征，具有這種特征的總體密度曲線一般可用下面函數(shù)的圖象來表示或近似表示：
，
式中的實(shí)數(shù)、是參數(shù)，分別表示總體的平均數(shù)與標(biāo)準(zhǔn)差，的圖象為正態(tài)分布密度曲線,簡稱 ．
2，一般地，如果對(duì)于任何實(shí)數(shù)，隨機(jī)變量X滿足
3、 ，
則稱 X 的分布為正態(tài)分布．正態(tài)分布完全由參數(shù)和確定，因此正態(tài)分布常記作 ．如果隨機(jī)變量 X 服從正態(tài)分布，則記為 .
2 / 3
說明:1參數(shù)是反映隨機(jī)變量取值的平均水平的特征數(shù)，可以用樣本均值去佑計(jì)；是衡量隨機(jī)變量總體波動(dòng)大小的特征數(shù)，可以用樣本標(biāo)準(zhǔn)差去估計(jì)．正態(tài)分布）是由均值μ和標(biāo)準(zhǔn)差σ唯一決定的分布
3．正態(tài)曲線的性質(zhì)：
（1）
（2）
4、
（3）
（4） 。
當(dāng)x＜μ時(shí)，曲線上升（增函數(shù)）；當(dāng)x＞μ時(shí)，曲線下降（減函數(shù)） 并且當(dāng)曲線向左、右兩邊無限延伸時(shí)，以x軸為漸近線，向它無限靠近
（5） 。
（6） ，
。
講解范例：例1．給出下列三個(gè)正態(tài)總體的函數(shù)表達(dá)式，請(qǐng)找出其均值μ和標(biāo)準(zhǔn)差σ
（１）
（２）
（３）
74頁練習(xí)1,3 75頁A組2
希望對(duì)大家有所幫助，多謝您的瀏覽！
河北省二十冶綜合學(xué)校高考數(shù)學(xué)總復(fù)習(xí) 正態(tài)分布教案
