《2018-2019學(xué)年八年級(jí)數(shù)學(xué)下冊(cè) 第十八章 平行四邊形 18.1 平行四邊形 18.1.1 平行四邊形的性質(zhì) 第2課時(shí) 平行四邊形的性質(zhì)3練習(xí) （新版）新人教版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2018-2019學(xué)年八年級(jí)數(shù)學(xué)下冊(cè) 第十八章 平行四邊形 18.1 平行四邊形 18.1.1 平行四邊形的性質(zhì) 第2課時(shí) 平行四邊形的性質(zhì)3練習(xí) （新版）新人教版（3頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、第2課時(shí) 平行四邊形的性質(zhì)3
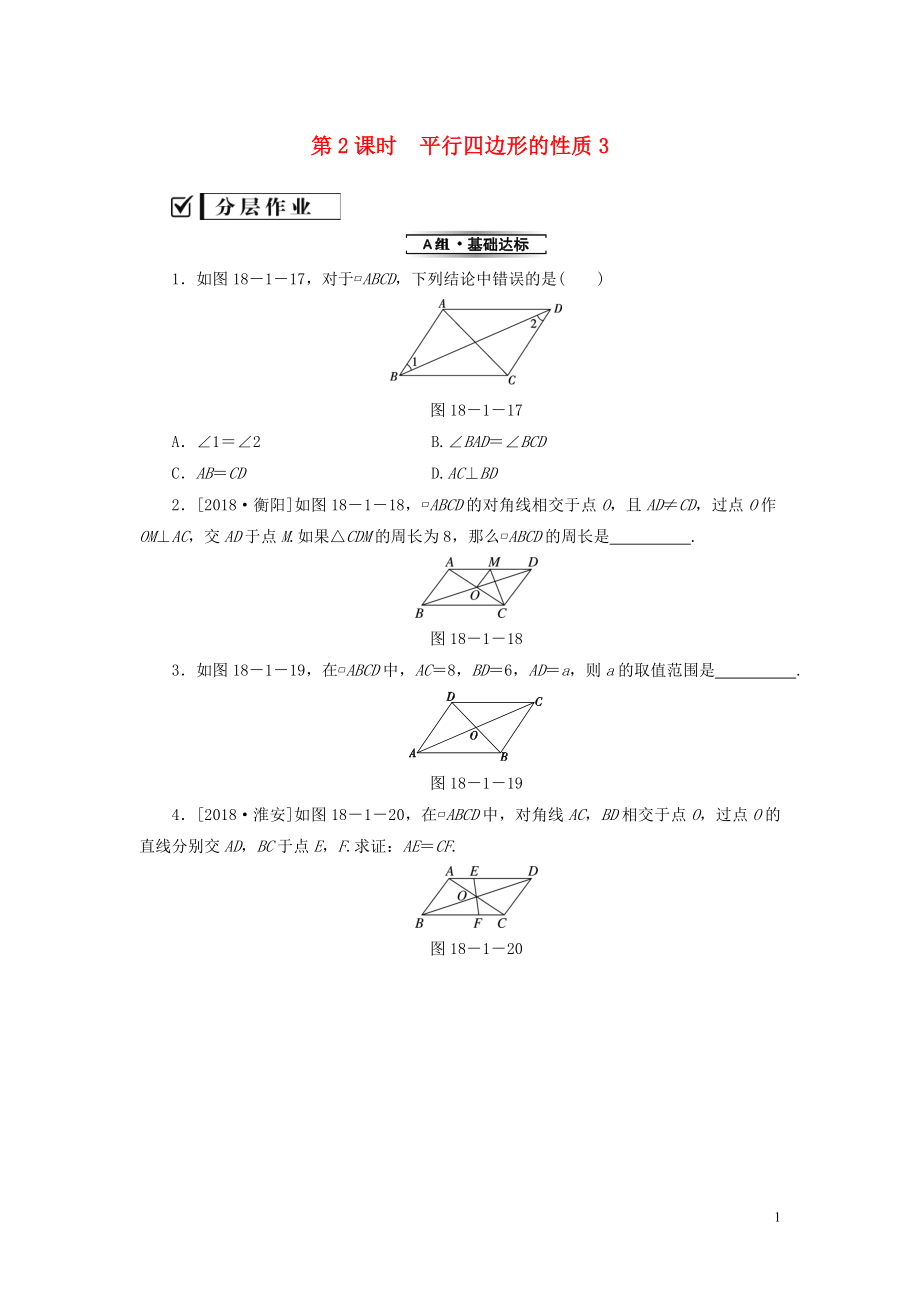
1．如圖18－1－17，對(duì)于?ABCD，下列結(jié)論中錯(cuò)誤的是( )
圖18－1－17
A．∠1＝∠2 B.∠BAD＝∠BCD
C．AB＝CD D.AC⊥BD
2．[2018·衡陽]如圖18－1－18，?ABCD的對(duì)角線相交于點(diǎn)O，且AD≠CD，過點(diǎn)O作OM⊥AC，交AD于點(diǎn)M.如果△CDM的周長(zhǎng)為8，那么?ABCD的周長(zhǎng)是 .
圖18－1－18
3．如圖18－1－19，在?ABCD中，AC＝8，BD＝6，AD＝a，則a的取值范圍是 .
圖18－1－19
4．[2018·淮安]如圖18
2、－1－20，在?ABCD中，對(duì)角線AC，BD相交于點(diǎn)O，過點(diǎn)O的直線分別交AD，BC于點(diǎn)E，F(xiàn).求證：AE＝CF.
圖18－1－20
5．如圖18－1－21，在?ABCD中，BD⊥AD，∠A＝45°，E，F(xiàn)分別是AB，CD上的點(diǎn)，且BE＝DF，連接EF交BD于點(diǎn)O.
圖18－1－21
(1)求證：BO＝DO；
(2)若EF⊥AB，延長(zhǎng)EF交AD的延長(zhǎng)線于點(diǎn)G，當(dāng)FG＝1時(shí)，求AE的長(zhǎng)．
6．[2018·黃岡]如圖18－1－22，在?ABCD中，分別以邊BC，CD作等腰△BCF，△CDE，使BC＝BF，CD＝DE，∠CBF＝∠CDE，連接AF，AE.
(1)求證：△ABF≌△EDA；
(2)延長(zhǎng)AB與CF相交于點(diǎn)G，若AF⊥AE，求證BF⊥BC.
參考答案
第2課時(shí) 平行四邊形的性質(zhì)3
【分層作業(yè)】
1．D 2.16 3.1＜a＜7 4.略
5．(1)略 (2)AE＝3 6.略
3
2018-2019學(xué)年八年級(jí)數(shù)學(xué)下冊(cè) 第十八章 平行四邊形 18.1 平行四邊形 18.1.1 平行四邊形的性質(zhì) 第2課時(shí) 平行四邊形的性質(zhì)3練習(xí) （新版）新人教版
